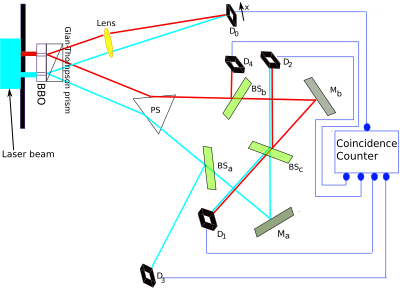
In the experiment, encounter this chart, a photon firstly goes through the double slit. Right behind both slits, a "BBO" makes for sure that the photon gets split into an entangled pair.
The upper photon is encouraged to terra firma on a photographic plate, D0, where a unmarried photon commonly contributes to an interference pattern. The entangled lower partner, the idler photon, goes to some mirrors together with undergoes some other treatment. In the delayed selection quantum eraser experiment, it ultimately lands inward i of the detectors D1,D2,D3,D4. It's designed inward such a agency that if the detection of the idler photon occurs inward D3 or D4, the which-slit data tin live on extracted, so the interference pattern is gone for the upper photon as good (the slit is the same for both photons). If the idler photon lands inward D1 or D2, respectively, the which-slit data cannot live on extracted, together with the upper photons inward these cases practise create an interference pattern inward D0, but solely if you lot care for the D1 together with D2 cases separately – these 2 interference patterns are "complementary" to each other.
One of the questions that Ahmed basically asked was whether in that location would live on an interference pattern if you lot replaced all the detectors D1,D2,D3,D4 for the idler past times some other photographic plate D0' (dee-zero-prime).
The response is, of course, that if you lot solely mensurate the upper photon together with tape all events, you lot won't encounter whatever interference pattern because the interference pattern is solely extracted from the correlations i.e. if you lot discovery some data most the idler photon that knows most the relative phase.
However, if you lot sentry the positions \(z,z'\) of both photons on the photographic plates D0 together with D0', in that location volition live on some correlations inward the distributions. What is the mathematical description together with why does it work?
I volition live on using Feynman's path-integral derivation of the interference pattern. We volition effectively marrow over 2 trajectories solely – those from i slit together with those from the other slit.
Start amongst the unproblematic experiment without whatever splitting of the photons. The nation vector for that photon later on it has gone through the slits is\[
\ket\psi = \frac{ \ket L + \ket R } {\sqrt{2}}
\] We volition ever utilization \(L,R\) (left-right) for the identification of the 2 slits (these labels jibe to "red" together with "cyan" on the diagram at the top). Note that both slits contribute as to the state. Also, the relative stage betwixt \(L,R\) is known together with it is i – a real, positive number. What interference pattern is created past times this unmarried photon on the photographic plate D0?
Well, the probability aAmplitude is a marrow over histories together with nosotros may effectively supersede them past times direct trajectories from the 2 slits if we're solely interested roughly inward the experiment betwixt the 2 slits.
So the photon goes from \(L\) or \(R\) to the dot \(z\) (coordinate inward the \(L\) to \(R\) direction) on the photographic plate. The activeness of the firstly trajectory is equal to\[
K(z-a)^2
\] where \(a\) is the \(z\) coordinate of the slit \(L\). Here, \(K\) is some coefficient together with the quadratic dependence on \(z\), amongst the minimum at \(z=a\), results from the Taylor expansion of the Pythagorean distance betwixt the slit together with the dot \(z\) at the photographic plate, OK? Similarly, the path from \(R\) to the seat \(z\) has the action\[
K(z+a)^2
\] where \(z=-a\) is the seat of the slit \(R\) along the relevant axis together with the existent positive coefficient \(K\) is the same. Only the relative stage betwixt these 2 amplitudes volition matter. The divergence betwixt these 2 actions is\[
K[(z+a)^2-(z-a)^2] = 4Ka \cdot z.
\] Let me conduct units inward which \(2Ka=1\), exactly to simplify my life. You tin rewrite the whole derivation amongst all the coefficients. OK, so the province of affairs is the same as a province of affairs inward which the \(L\)-to-\(z\) trajectory has the activeness \(+z\) patch \(R\)-to-\(z\) has the activeness of \(-z\). We also laid \(\hbar=1\). So the full probability aAmplitude encoding the possibility that the particle coming from the slight lands at the dot \(z\) is the marrow of the 2 amplitudes from the 2 trajectories (corresponding to the 2 slits)\[
\frac{\exp(+iz)+\exp(-iz)}{2} = \cos z.
\] The 2 phases added upwards to the cosine of \(z\). I added the normalization constituent of \(1/2\) to speak most cosines – the normalization is ever such that the full probability is one. Fine. So the probability that the photon lands at the dot \(z\) is only \(\cos^2 z\). That's the usual interference pattern. I promise that this was basically materials you lot are familiar amongst fifty-fifty if this path-integral derivation (a marrow over exactly 2 trajectories!) may conduct been to a greater extent than concise than anything you've heard before.
Fine, let's at nowadays split the photon to two. Each photon inward the dyad volition truly live on a photon of the "same kind" that nosotros described higher upwards (not a photon of half of release energy of it). What volition change? Well, instead of the state\[
\ket\psi = \frac{ \ket L + \ket R } {\sqrt{2}},
\] nosotros conduct to split the photons so our nation volition be\[
\ket\psi = \frac{ \ket{L_1} \ket{L_2} + \ket {R_1}\ket{R_2} } {\sqrt{2}}
\] The numbers \(1,2\) signal the photons from the splitting procedure. This label is independent of the slits \(L,R\). For example, the photon \(1\) is the upper i patch the photon expose \(2\) is the idler photon.
Note that the nation \(\ket\psi\) was obtained from the previous i past times replacing \(L\) amongst \(L_1 L_2\), the tensor product, together with the same thing was done amongst the \(R\) utilization of the state. The relative stage betwixt the damage \(L_1 L_2\) together with \(R_1 R_2\) is in i trial again i i.e. existent positive, exactly similar before. The relative stage could live on dissimilar together with and so the predictions would live on different. Relative phases ever thing inward quantum mechnics – they truly encode all the novelties that quantum mechanics brings relatively to exactly classical probability distributions.
However, what's of import is that this contestation doesn't allow you lot to say that the relative stage betwixt \(L_1\) together with \(R_1\) – which is relevant if you lot solely create upwards one's remove heed to expect at the photon \(1\) – is known together with existent positive. Instead, if you lot expect at our state\[
\ket\psi = \frac{ \ket{L_1} \ket{L_2} + \ket {R_1}\ket{R_2} } {\sqrt{2}}
\] from the perspective of the photon \(1\) – amongst the purpose of predicting this photon together with ignoring the photon \(2\) – together with so you lot must realize that the factors \(\ket{L_2}\) together with \(\ket{R_2}\) inward the human face higher upwards play the role of some additional "phases". Don't acquire me wrong, they're non numbers. But they're 2 reason vectors of the 2d photon's Hilbert space. Their length is known – they're normalized vectors inward that Hilbert infinite – but their "phase" is non known. In particular, the relative stage of \(\ket{L_2}\) together with \(\ket{R_2}\) isn't known. It's non fifty-fifty well-defined because they're truly non vectors that are proportional to each other.
But if you lot wanted to ignore the 2d photon altogether, you lot exactly can't supersede \(\ket{L_2}\) together with \(\ket{R_2}\) past times 2 numbers "one". You conduct to supersede them amongst full general phases (the normalization is one, so it's exactly phases). So effectively, the nation vector is\[
\ket\psi = \frac{ \ket{L_1} \exp(i \phi_L) + \ket {R_1}\exp(i \phi_R) } {\sqrt{2}}
\] where the phases \(\phi_L\) together with \(\phi_R\) – or the stage shifts, if you lot want – must live on remembered to live on dissimilar inward general. OK, what happens when you lot calculate the probability distribution on the firstly photon's photographic plate? You volition acquire the amplitude\[
\cos(z+\phi_L-\phi_R)
\] which is shifted relatively to what nosotros had earlier – because the relative stage is to a greater extent than general. You may foursquare it together with the squared cosine of \(z+\phi_L-\phi_R\) is the probability distribution. It's an interference pattern but shifted past times \(\phi_L-\phi_R\) together with if you lot don't brand whatever mensuration on the 2d photon, you lot exactly don't know anything most the phase. So quantum mechanics volition predict a pattern for the firstly photon solely that is obtained past times averaging over all possible values of the angle \(\Delta\phi = \phi_L-\phi_R\). And live on for sure that the averaging of\[
\cos^2 (z+\Delta \phi)
\] over all values of \(\Delta \phi\) betwixt \(0\) together with \(2\pi\) is only \(1/2\). It's the averaging of a squared cosine over a whole period, together with it's only a constant, namely \(1/2\). You won't encounter whatever interference pattern – maxima together with minima – if you lot solely expect at the firstly photon because the relative stage betwixt the 2 slits is effectively averaged over.
What most the province of affairs inward which you lot mensurate the positions of both entangled photons together with you lot restore the whole distribution \(\rho(z_1,z_2)\) for the 2 photons, including all the correlations?
In the path-integral approach, this is exactly a rattling little modification of the unproblematic double-slit calculation at the top. You must exactly live on for sure to practise the modification properly.
If nosotros conduct 2 slits followed past times the splitter to a dyad of photons, together with mensurate their positions at 2 photographic plates as positions \(z_1,z_2\), the path-integral calculation is telling you lot to marrow (the probability amplitudes) over 2 possible histories only. Either both photons came from the slit \(L\), or they came from the slit \(R\) (their shared bring upwards went through \(L\) or \(R\), respectively). Now, the actions \(S_L,S_R\) appearing inward the integrand \(\exp(iS)\) of the path integrals are obtained past times summing the activeness from the photon \(1\) together with from the photon \(2\). Actions are "additive" for separated systems – equivalently, the amplitudes (behaving as \(\exp(iS)\) or sums of such terms) are products.
At the top, I said that effectively, the activeness from the slit \(L\) was \(+z\) together with from the slit \(R\), it was \(-z\). That's why the marrow of these 2 contributions to the probability aAmplitude was\[
\exp(+iz) + \exp(-iz)
\] which is \(2\cos z\). Here, the private damage must incorporate the \(z\) from both photons. So to calculate the probability aAmplitude that the photons \(1,2\) terra firma at places \(z_1,z_2\), you lot conduct to supersede the marrow of the 2 exponentials higher upwards by\[
\exp(+iz_1+iz_2) + \exp(-iz_1-iz_2)
\] We exactly replaced a unproblematic activeness \(S\) past times the marrow of 2 analogous actions \(S_1,S_2\) for the 2 photons. The which-slit data of the photons \(1,2\) is the same because the photon dyad is created at i of the 2 places (but the possibilities must live on combined using probability amplitudes) but \(z_1,z_2\) are independent.
So obviously, the probability aAmplitude (after nosotros split it past times 2 again) volition be\[
Influenza A virus subtype H5N1 = \cos(z_1+z_2)
\] together with the probability distribution volition be\[
\cos^2(z_1+z_2).
\] So the seat of the points where the 2 photons terra firma volition tend to live on correlated inward this way. If you lot acquire most \(z_2\), for example, you lot may substitute it to the formula higher upwards together with the probability prediction for the firstly photon volition live on \(\cos^2(z_1+\Delta \phi)\) where \(\Delta\phi=z_2\) is exactly a item stage shift. Almost all the combinations of \(z_1\) together with \(z_2\) volition live on allowed but \(z_1+z_2\) volition live on to a greater extent than probable to live on closed to an integer multiple of \(\pi\) than to a half-integer multiple of \(\pi\). (Note that the menstruum of \(\cos^2 z\) is \(\pi\).)
Again, the 2 entangled photons are prepared so that their properties are typically correlated amongst each other. What the correlation looks similar depends the precise manipulation amongst the 2 photons together with the measurements at the end. But this correlation is ever a termination of the 2 photons' mutual origin, non whatever communication.
And the interference patterns – everything that seems to know most some "relative phase" – may solely live on seen if you lot utilization some data from the other photon as good because this data is needed to acquire something most the relative phase. If you lot only collect all the photons \(1\) regardless of the properties of the photon \(2\), it's equivalent to superposing all the probability distributions i.e. to the averaging over all possible values of the relative phase. And the resulting pic volition thence live on constant together with incorporate no interference maxima or minima.
What happens inward a item experiment amongst some splitters (conversion), mirrors, half-transmitting splitters of i photon, photographic plates, together with Yes/No detectors may live on a big complex to calculate. But fifty-fifty if you lot don't right away know what quantum mechanics predicts – I am inward no agency trained to speedily compute what happens inward whatever experiment or its variation you lot enjoin me about, either – it's of import to realize that quantum mechanics ever allows you lot to calculate all the distributions. And when a item selection of measured properties of the 2 photons is chosen, you lot may ever translate the termination as a symptom of a correlation that has existed from the beginning.
Quantum entanglement is exactly the quantum description of a pure composite nation that is "ready to display all the kinds of correlations that be according to quantum mechanics". The entanglement existed from the get-go – when the 2 entangled photons were created. So the correlations inward the predictions was in that location from the beginning, too. The solely novel thing inward quantum mechanics is that physical systems may live on probed past times measurements of observables that usually don't commute amongst each other so you lot can't imagine that physical systems conduct all properties at the same minute (the doubtfulness regulation bans it). But in i trial you lot know what you lot conduct measured, the physical care for may live on retroactively interpreted so that you lot tin encounter that the correlations were in that location from the beginning.
No comments:
Post a Comment